Теория механизмов и машин

Сопряженные профили

На рисунке сопряженный профиль шестерни имеет красный цвет, а колеса - зеленый. Построение сопряженного профиля проводится следующим образом:

• В месте пересечения окружности вершин колеса и линии зацепления \(N_{1}N_{2}\) отмечается точка \(B_2\);
• Из центра шестерни проводится дуга из точки \(B_2\) до пересечения с профилем зуба шестерни в зацеплении. Радиус дуги - радиус активного профиля шестерни \(r_{p1}\);
• Выделяется штриховкой активный профиль шестерни;
• Аналогично проводится активный профиль колеса.

Контактная точка

Точка, где происходит сопряжение профилей в конкретный момент времени и профили имеют общую касательную, называется точкой контакта \(K\). В процессе взаимодействия профилей она перемещается вдоль активного участка линии зацепления \(B_{2}B_{1}\) от точки \(B_2\) до точки \(B_1\), если шестерня вращается против часовой стрелки. И наоборот, от точки \(B_1\) к \(B_2\), если шестерня вращается по часовой стрелке.

Если точка контакта \(K\) выходит за пределы активного участка линии зацепления, возникает явление заклинивания.

Полюс зацепления

Точка пересечения нормали к касательной, проведенной через точку контакта \(K\), и линии, соединяющей центры шестерни и колеса, называется полюсом зацепления \(P\). Также полюс зацепления находится в точке касания начальных окружностей \(r_{w1}\) и \(r_{w2}\) и в точке пересечения линии зацепления и линии, соединяющей центры шестерни и колеса.

Для зубчатых передач с постоянным передаточным отношением полюс зацепления \(P\) не меняет своего положения в процессе взаимодействия профилей.

Передаточное отношение

Основная теорема зацепления:

Линия зацепления в полюсе зацепления \(P\) делит отрезок, соединяющий центры шестерни и колеса, на части, соответствующие угловым скоростям, с которыми движутся шестерня и колесо. Отношение большего отрезка к меньшему - передаточное отношение.

$$U_{12}=\dfrac{n_1}{n_2}=-\dfrac{r_{w2}}{r_{w1}}=-\dfrac{Z_2}{Z_1}$$

где:

• \(n_1,\;n_2\) - частоты вращения шестерни и колеса;
• \(r_{w1},\;r_{w1}\) - радиусы основных окружностей шестерни и колеса;
• \(Z_1,\;Z_2\) - числа зубьев шестерни и колеса.

Параметры исходного производящего контура

• \(h_{f}=h_{f}^{*}\cdot m\) - высота ножки зуба инструмента;
• \(h_{a}=h_{a}^{*}\cdot m\) - высота головки зуба инструмента;
• \(h_{f}^{*},\;h_{a}^{*}\) - соответствующие коэффициенты;
• \(h_{0}\) - высота зуба инструмента;
• \(\alpha\) - угол главного профиля;
• \(\rho_{f}\) - радиус кривизны переходной кривой;
• \(C=C^{*}\cdot m\) - радиальный зазор;
• \(C^{*}\) - коэффициент радиального зазора;
• \(P=\pi\cdot m\) - шаг инструмента;
• \(s=\dfrac{P}{2}\) - толщина зуба инструмента;
• \(e=\dfrac{P}{2}\) - толщина впадины инструмента;

Сопряженные поверхности

Сопряженными называют поверхности, по которым происходит взаимодействие профилей зубчатых колес. О сопряженном профиле подробно изложено в Вопросе 1.

Производящая поверхность

Производящей называют поверхность, образованную в результате движения профиля режущего инструмента. Производящая поверхность изображена на рисунке. Ее построение проводится следующим образом:

• Из точки \(B_1\), полученной пересечением линии станочного зацепления и окружности вершин шестерни, проводят горизонтальную линию до пересечения с профилем инструмента;
• Отмечают производящую поверхность штриховкой.

Зубчатое зацепление

Под зубчатым зацеплением понимают взаимодействие двух зубчатых колес, причем контакт боковых поверхностей зубьев должен обеспечиваться пятиподвижной точечной парой. В случае применения колес с линейным контактом зубьев (четырехподвижная линейная пара) возникает одна избыточная связь.

В зубчатом зацеплении начальными являются начальные окружности шестерни \(r_{w1}\) и колеса \(r_{w2}\).

Станочное зацепление

Станочное зацепление - взаимодействие заготовки зубчатого колеса и режущего производящего инструмента.

В станочном зацеплении начальными линиями являются станочно-начальная прямая и делительная окружность \(r_1\) заготовки зубчатого колеса (см. рисунок).

Свойства эвольвенты

• Нормаль к эвольвенте в каждой точке касается основной окружности.

• Ниже основной окружности эвольвентного профиля не существует.

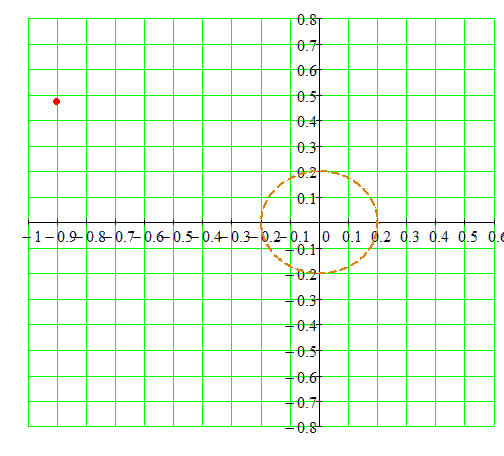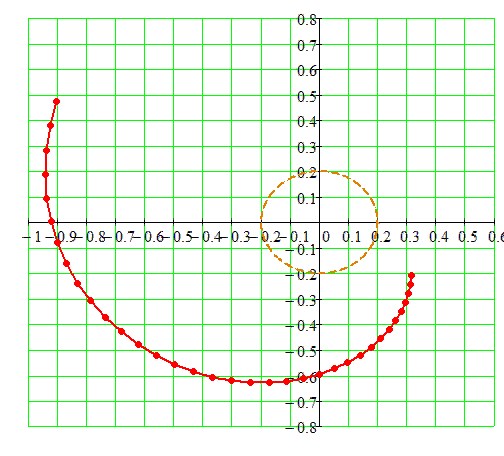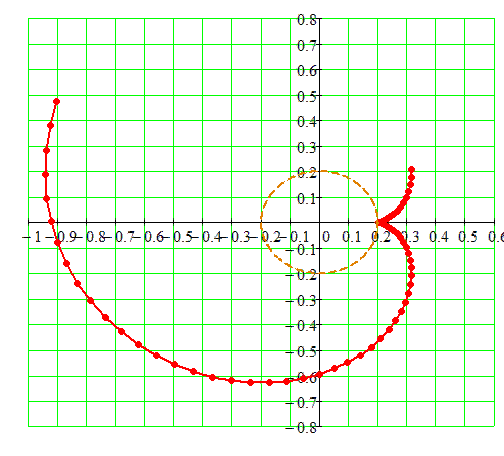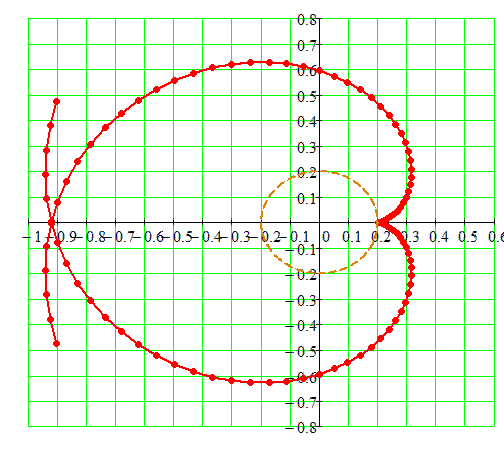
• Радиус кривизны эвольвенты в каждой точке равен длине отрезка касательной к основной окружности. Радиус кривизны равен отрезку \(KN_1\) (см. рисунок выше).

Свойства эвольвентного зацепления

• Отношение радиусов основных окружностей и отношение радиусов начальных окружностей - передаточное отношение зубчатой передачи.

• Произведение величины межосевого расстояния и косинуса угла зацепления остается постоянным при любом значении межосевого расстояния.

• \(\alpha_{w}\) - угол зацепления; \(a_{w}\) - межосевое расстояние.

Положение исходного производящего контура оказывает влияние на коэффициент смещения.

Коэффициент смещения - величина, равная отношению смещения производящего исходного контура к нормальному модулю цилиндрического зубчатого колеса. В зависимости от величины и знака этого смещения различают зубчатые передачи:

• Положительные - составленные из колес с положительными смещениями или когда положительное смещение одного колеса больше отрицательного смещения другого (рис. а).
• Нулевые или равносмещенные - составленные из зубчатых колес без смещения или с равными, но противоположными по знаку смещениями (рис. б).
• Отрицательные - составленные из колес с отрицательными смещениями или когда отрицательное смещение одного колеса больше положительного смещения другого (рис. в).

Чем больше коэффициент смещения, тем большие габариты будет иметь проектируемая передача. При этом толщина зуба по окружности вершин будет уменьшаться вплоть до возникновения заострения.

Чем меньше коэффициент смещения, тем меньше будут габариты проектируемой передачи. При этом будет происходит утоньшение ножки зуба, вплоть до возникновения подрезания.

Рассмотрение и анализ качественных показателей подробно проведены тут.

Методы изготовления

• Обкатка - заготовка находится в зацеплении с тремя закаленными калиброванными зубчатыми колесами, изготовленными с высокой степенью точности и чистоты поверхности. Процесс происходит с вращением колес в одну сторону, а затем в другу. Обкатка осуществляется на незакаленном металле. Станочное зацепление в курсовом проекте было построено методом обкатки реечного инструмента.
• Копирование - процесс фрезерования заготовки специальной фрезой, при котором перемещение инструмента происходит с определенным шагом, соответствующим угловому шагу изготавливаемого колеса.
• Накатка - формирование профиля более твердого колеса на заготовке из более мягкого материала.

На иллюстрации выше выделены угол рабочего зацепления \(\alpha_w\) и угол станочного зацепления \(\alpha_{w0}\). Угол станочного зацепления всегда равен углу профиля Исходного Производящего Контура \(\alpha\) (для стандартного инструмента \(\alpha=20^{\circ}\)). Угол рабочего зацепления может принимать различные значения и зависит от межосевого расстояния.

Для станочного зацепления делительная окружность шестерни совпадает с начальной окружностью и касается станочно-начальной прямой в полюсе станочного зацепления \(P_0\). Отсюда следует условие совпадения угла рабочего и станочного зацепления:

Для равенства углов станочного и рабочего зацеплений необходимо, чтобы колеса, входящие в зацепление, имели суммарное смещение, равное 0. При этом коэффициент уравнительного смещения \(y=0\) и уравнительное смещение \(y\cdot m=0\). Кроме того, совпадают делительные и начальные окружности у шестерни и колеса.

Угол профиля - угол между касательной к эвольвенте и отрезком, соединяющим центр колеса с точкой, в которой определяется данный угол.

Нахождение угла профиля в определенной точке:

Способ 1 (на рисунке отмечен красным цветом)

• Проводится касательная к эвольвенте в этой точке;
• Из центра колеса проводится отрезок к этой точке;
• Угол между касательной и проведенным отрезком - угол профиля.

Способ 2 (на рисунке отмечен синим цветом)

• Из центра колеса проводится отрезок к этой точке;
• Проводится касательная к основной окружности из этой точки;
• Точка касания соединяется отрезком с центром колеса;
• Угол между проведенными отрезками - угол профиля.

К основным параметрам зацепления относятся:

• Межосевое расстояние \(A_w\): $$A_w=R_{w1}+R_{w2}$$
• Передаточное отношение \(U_{12}\): $$U_{12}=-\dfrac{R_{w2}}{R_{w1}}=-\dfrac{Z_2}{Z_1}$$
• Угол зацепления \(\alpha_w\);
• Воспринимаемое смещение \(y\cdot m\)

Чаще всего передаточное отношение задано, и его требуется обеспечить. Остальные параметры зависят от:

• Требуемого передаточного отношения;
• Модуля;
• Коэффициента воспринимаемого смещения, который определяется принимаемыми коэффициентами смещения \(X_1;\;X_2\)

Подрезание - негативное последствие, возникающее, когда точка B_l активного участка линии зацепления выходит за границы зоны сопряженного контакта \(B_{l}N\). Возникновение подрезания происходит при неграмотном выборе коэффициента смещения в том случае, когда не выполняется условие:

где

\(\alpha\) - угол главного профиля;

\(Z\) - число зубьев проектируемого зубчатого колеса;

\(h_{a}^{*}\) - коэффициент высоты головки зуба.

Иллюстрация возникновения подрезания при изменении коэффициента смещения проектируемого колеса:

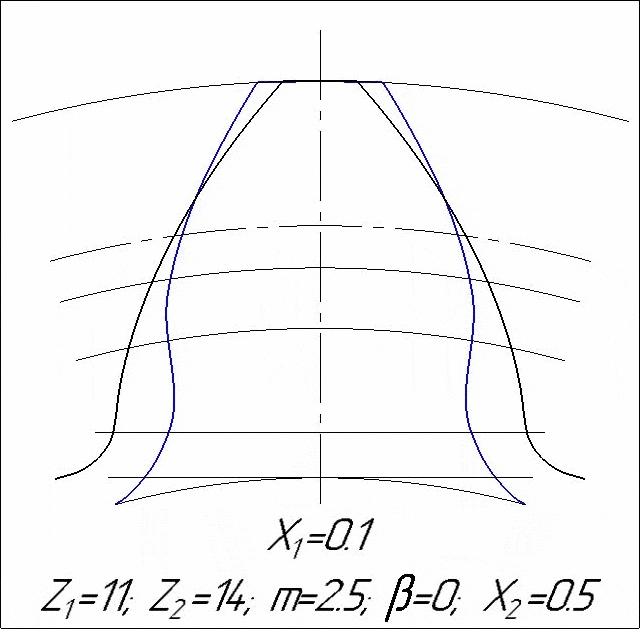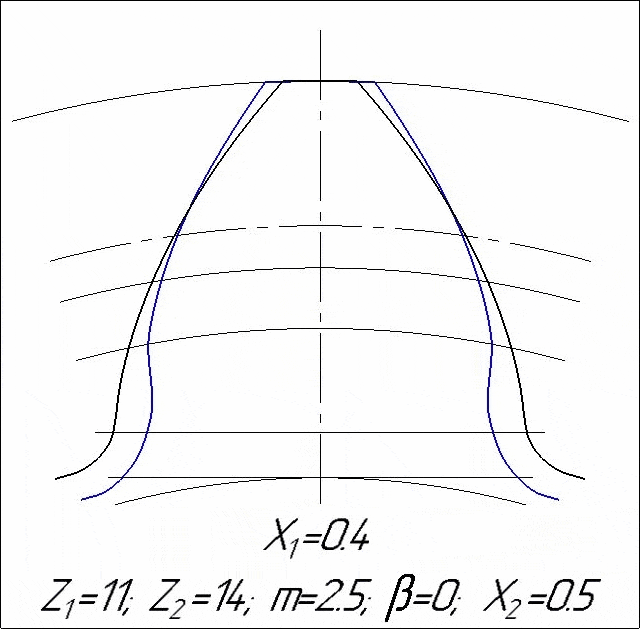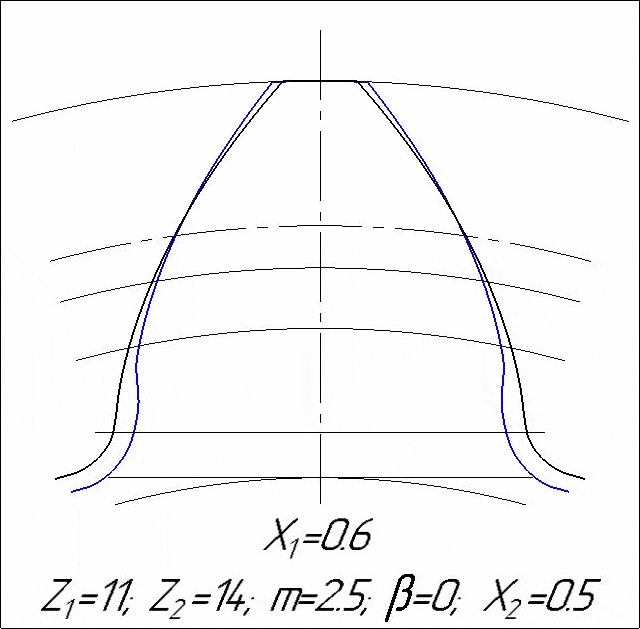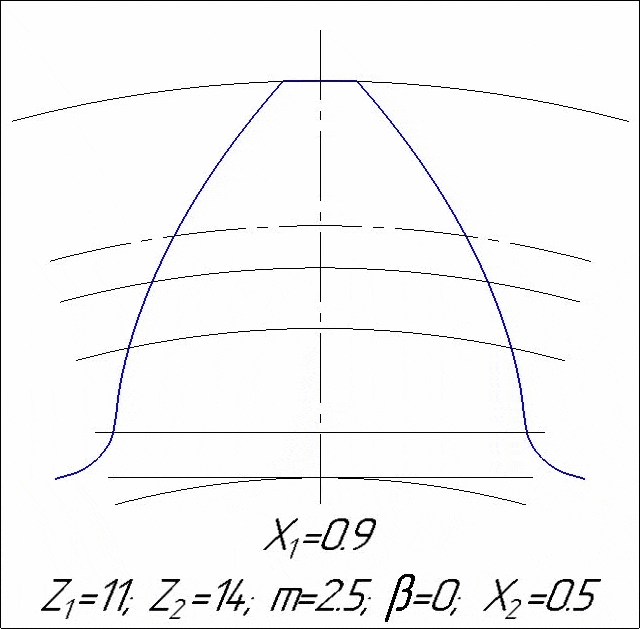
Отрезки, характеризующие смещение инструмента

Радиальному смещению соответствует отрезок \(GP_0\). Смещение вдоль линии зацепления (контактной линии)- отрезок \(KK'\). Смещение вдоль профиля - участок эвольвенты между точками \(K''K\). При построении смещений линия зацепления смещается на величину радиального смещения и \(GP_0=P_0G'\).

Подрезание возникнет в том случае, если точка \(B_2\) будет ниже точки \(N_1\). Расстояние между точками \(N_1B_2'\) характеризует запас по величине радиуса основной окружности до возникновения подрезания.

Линия зацепления - линия, вдоль которой движется точка контакта \(K\). Линия станочного зацепления - касательная к основной окружности шестерни. Линия эвольвентного зацепления одновременно является касательной к основным окружностям шестерни и колеса.

Линии зацепления имеют активные участки, ограниченные точками \(B_1\) и \(B_2\). В этих точках пара зубьев шестерни и колеса (или шестерни и инструмента) входит и выходит из зацепления.

Длина активного участка линии зацепления зависит от:

• Передаточного отношения \(U_{12}\);
• Межосевого расстояния \(A_w\);
• Угла профиля \(\alpha\) и угла зацепления \(\alpha_w\);
• Коэффициента перекрытия \(\varepsilon\) (коэффициента смещения).

Чем больше коэффициент смещения, тем меньше коэффициент перекрытия.

Для цилиндрических колес различают:

• полное \(\varepsilon_{\gamma}\)
• торцевое \(\varepsilon_{\alpha}\)
• осевое перекрытие \(\varepsilon_{\beta}\)

Коэффициент торцевого перекрытия \(\varepsilon_{\alpha}\) может быть определен следующим образом:

где

\(\alpha\) - угол главного профиля исходного контура; \(g_{\alpha f}+g_{\alpha b}\) - длина активного участка линии зацепления.

Обозначения \(l_{B_1N_2}, l_{PN_2}\) и т. д. - длины с чертежа.

Коэффициент перекрытия определяет величину зоны контакта двух пар зубьев, когда одновременно зацепляются два последовательно расположенных зуба. Так как до окончания зацепления одной пары зубьев следующая пара должна войти в контакт, в прямозубых передачах следует обеспечивать \(\varepsilon_\alpha\geq1.05...1.25\).

Допустимое значение коэффициента перекрытия выбирается исходя из назначения передачи и точности ее изготовления. Максимальное значение коэффициента перекрытия для зубчатых колес, обработанных инструментом со стандартным исходным производящим контуром, составляет \(\varepsilon_\alpha=1.98\).

Коэффициенты удельного скольжения \(\lambda_1, \lambda_2\) характеризуют скольжение при геометрических расчетах зубчатой передачи, которые, в свою очередь, определяют величину износа активного профиля в высшей кинематической паре. Износ шестерни с увеличение коэффициента смещения уменьшается, и, наоборот, очень быстро увеличивается при приближении к минимальному значению этого коэффициента. Зависимость изменения износа колеса меняется не сильно в области рассматриваемых значений коэффициентов смещения шестерни.

Чем больше скольжение, тем быстрее будет происходить износ зубчатого колеса.

Коэффициент удельного скольжения зависит от:

• Межосевого расстояния \(A_w\);
• Передаточного отношения \(U_{12}\);
• Коэффициента смещения \(X\).

По чертежу данный коэффициент для точки \(B_2\) определяется следующим образом:

Коэффициент удельного давления \(\nu\) характеризует влияние формы зуба на контактную прочность и используется для оценки контактных напряжений в высшей кинематической паре. В курсовом проекте по ТММ в месте контакта зубьев происходит сухое трение, поэтому данный коэффициент изменяется незначительно при любом значении коэффициента смещения.

Чем больше коэффициент удельного давления, тем более интенсивно происходит выкрашивание металла с поверхности зубьев (питтинг) и снижается ресурс этого зубчатого колеса в зацеплении.

Для снижения контактных напряжений следует увеличить коэффициент смещения.

Аналитически коэффициент удельного давления рассчитывается по формуле:

Из первой дроби следует тот факт, что данный коэффициент не зависит от модуля, т. е. габаритов зубчатого колеса, а зависит от его качественных параметров.

Графически коэффициент удельного давления рассчитывается по формуле:

Здесь: \(N_1N_2\) - длина линии зацепления; \(m_t\) - торцевой модуль; \(N_1K\) и \(N_2K\) - радиусы кривизны эвольвентного профиля шестерни и колеса соответственно.

Выбор коэффициентов смещения проводился после определения Области Допустимых Значений (ОДЗ). Данная область образуется за счет ограничения по подрезанию слева и за счет ограничения по заострению справа. Подробно анализ качественных показателей и выбор коэффициентов смещения мы рассмотрели здесь.

Запас по смещению можно определить по схеме станочного зацепления.

Подрезание зуба шестерни не будет происходить, если точка \(B_2\), ограничивающая активную линию зацепления, лежит выше точки \(N_1\). Расстояние между точками \(N_1B_2'\) характеризует запас по условию подрезания в радиальном направлении.

Данный вопрос нацелен на проверку знания алгоритма построения станочного зацепления методом обращенного движения. Алгоритм построения подробно изложен в разделе построение станочного зацепления.

Для определения траекторий точек исходного контура в обращенном движении следует обратить внимание на 15-19 шаги. В 19 шаге осевой линией проводятся траектории точки контура, лежащей на линии граничных точек и траектория центра скругления. Поскольку профиль ИПК - отрезок прямой, то двух точек достаточно для построения контура в каждый момент обращенного движения.

Сопряженная (в случае станочного зацепления - производящая) поверхность находится на 26-27 шагах.

Сложным зубчатым механизмов называют механизм с числом колес, большим двух. Примерами сложных зубчатых механизмов являются редуктор, известный вам из курса Детали машин; планетарные редукторы; дифференциалы.

Планетарный редуктор - редуктор, содержащий хотя бы одно колесо, ось которого подвижна. Такое колесо называют сателлитом.

Дифференциалом называют устройство, способное не только преобразовывать частоту вращения и момент на валу, но и разделять или объединять два и более потока мощностей. Такие механизмы применяются в автомобилях для обеспечения разной скорости вращения ведущих колес на поворотах.

Для определения числа степеней свободы (числа независимых движений) применяют формулу Сомова-Малышева для пространственных механизмов и формулу Чебышева для плоских механизмов.

Формула Сомова-Малышева:

Формула Чебышева:

Здесь: \(n\) - число подвижных звеньев; \(p_н\) - число низших кинематических пар (одна подвижность); \(p_в\) - число высших кинематических пар (две подвижности); \(q\) - избыточные связи.

Для низших кинематических пар обеспечивается точечный контакт, а для низших - по линии или поверхности.

Зубчатая передача

Зубчатые колеса закреплены на валах с образование вращательной одноподвижной пары в случае плоского механизма. Поэтому:

• Общее число элементов \(n_{общ}=3\) (валы - образующие стойку, два зубчатых колеса);
• Число подвижных элементов \(n=2\);
• Кинематические пары:
  • Стойка и шестерня - низшая;
  • Стойка и колесо - низшая;
  • Шестерня и колесо - высшая;

Тогда для плоского механизма:

Планетарный редуктор

Для однорядного планетарного редуктора:

• Число подвижных звеньев \(n=5\) (3 сателлита, водило, солнце);
• Кинематические пары:
  • 3 внешних зацепления сателлитов и солнца - высшие;
  • 3 внутренних зацепления сателлитов и эпицикла - высшие;
  • 3 связи водила и сателлитов - низшие;
  • Водило и стойка - низшая;
  • Солнце и стойка - низшая;
  • Эпицикл и стойка - низшая;

Тогда по формуле Чебышева:

У планетарного редуктора с 3 сателлитами число избыточных связей \(q=4\), а у планетарного редуктора с 1 сателлитом избыточных связей нет.

Подробно алгоритмы построения планов скоростей для планетарных редукторов мы рассмотрели в разделе.

Отметим, что угловая скорость звена направлена в ту сторону, в которую направлен вектор скорости какой-либо точки на этом звене.

Максимальную угловую скорость в абсолютном движении будет иметь солнечное колесо. В относительном движении наибольшую угловую скорость будет иметь сателлит, относительно водила, т. к. их скорости направлены в разные стороны.

Этот вопрос является продолжением вопроса 19. Для ответа на него следует обратиться в раздел.

Мгновенные центры скоростей были использованы для определения передаточных отношений графическим методом Л. П. Смирнова.

Графически коэффициент перекрытия определяется по формуле:

Коэффициенты перекрытия в станочном и рабочем зацеплении относятся как:

Т. к. активный участок линии станочного зацепления больше чем активный участок линии рабочего зацепления, то и коэффициент перекрытия в станочном зацеплении больше.

Длина активного участка линии зацепления зависит от:

• Передаточного отношения \(U_{12}\);
• Межосевого расстояния \(A_w\);
• Угла профиля \(\alpha\) и угла зацепления \(\alpha_w\);
• Коэффициента перекрытия \(\varepsilon\) (коэффициента смещения).

Коэффициент перекрытия больше в том зацеплении, в котором меньше коэффициент воспринимаемого смещения.

Для определения угла профиля необходимо:

• В вершину зуба провести радиус-вектор из центра колеса;
• Провести касательную к эвольвентному профилю в вершине зуба;
• Угол профиля - угол между проведенной касательной и радиус вектором.

Для определения инволюты угла профиля следует:

• Провести отрезок из центра колеса в точку начала эвольвентного профиля на основной окружности;
• В вершину зуба провести радиус-вектор из центра колеса;
• Угол между радиус-вектором и проведенным отрезком - инволюта угла профиля у вершины зуба.

Инволюта угла профиля - угол, на который развернулась эвольвента при данном угле профиля.

Алгоритм определения положения точки, сопряженной заданной:

• На профиле шестерни произвольно отмечается точка \(1\);
• Из центра шестерни проводится дуга радиусом \(r_{т1}\) от точки \(1\) до пересечения с линией рабочего зацепления в точке \(2\);
• Из центра колеса проводится дуга радиусом \(r_{т2}\) от точки \(2\) до пересечения с профилем зуба колеса в точке \(3\)

Данный алгоритм может быть применен и при решении обратной задачи, когда требуется определить сопряженную точку для точки, лежащей на профиле колеса.

Место контакта этих двух точек на линии зацепления - точка \(2\).

В месте пересечения линии станочного зацепления и линии граничных точек инструмента ставится точка \(B_2\), которая ограничивает активный участок линии станочного зацепления.

Для наглядности найдем проекции точек \(B_2\) и \(N_1\) на ось симметрии зуба в станочном зацеплении и отметим точки \(B_2'\) и \(N_1'\). Расстояние между этими точками \(B_2'N_1'\) - разность между выбранным и минимальным смещением.

Уравнительное смещение характеризует удельную величину радиального зазора, т. е. данная величина должна быть больше нуля для избежания интерференции (пересечения) вершины и впадины зубьев в зацеплении.

Здесь \(y\) - коэффициент воспринимаемого смещения; \(\Delta y\) - коэффициент уравнительного смещения; \(X_1;\;X_2\) - коэффициенты смещения шестерни и колеса соответственно.

Одним из условием выбора коэффициента смещения шестерни \(X_1\) было обеспечение значения коэффициента торцевого перекрытия \(\varepsilon_{\alpha}\geqslant1.05\). Это значит, что на момент выхода пары зубьев из зацепления очередная пара зубьев уже находится в зацеплении.

Ответом на вопрос является нахождение точек, в которых происходит зацепление очередной пары зубьев, пока в зацеплении еще находится предыдущая пара зубьев.

Алгоритм нахождения точек пересопряжения для колеса:

• Проведем радиус-векторы в вершину левого зуба и в точку входа зуба в зацепление, как показано на иллюстрации синими пунктирными линиями;
• Поворачиваем оба вектора так, чтобы конец нижнего вектора оказался в точке \(B_1\), как показано на иллюстрации синими сплошными линиями;
• В месте пересечения верхнего радиус-вектора с линией зацепления отмечаем точку \(C'\) - точку пересопряжения профилей.

После выхода пары зубьев из зацепления следующая пара будет находиться в точке пересопряжения \(C'\).

Аналогично проводим построения для шестерни и определяем вторую точку пересопряжения \(C''\).

Точка \(C''\) характеризует положение первой пары зубьев в момент вхождения следующей пары зубьев в зацепление.

Для ответа на вопрос следует внимательно посмотреть на иллюстрацию:

Увеличение коэффициента смещения приводит к тому, что толщина зуба по окружности вершин становится меньше, а по делительной окружности, совпадающей для станочного зацепления с начальной, больше.

Для удобства рассмотрим точку, лежащую на вершине зуба.

• Через требуемую точку проводим отрезок, касательный к основной окружности - радиус кривизны эвольвентного профиля в данной точке.
• В точке пересечения линии симметрии зуба и проведенного отрезка проводим перпендикуляр к линии симметрии зуба. Угол между перпендикуляром и отрезком касательной - угол давления в данной точке.
• Проводим касательную к эвольвентному профилю в данной точке, линию симметрии зуба перемещаем параллельным переносом в эту же точку. Угол между касательной и перенесенной линией симметрии зуба - угол эвольвентного профиля в данной точке.
• Проводим радиус-векторы из центра колеса в данную точку и в точку начала эвольвенты на основной окружности. Угол между радиус векторами - инволюта угла профиля в данной точке.

В качестве примера рассмотрим точку контакта \(K\) и определим скорость скольжения в ней. Алгоритм нахождения скорости скольжения в точке:

• Из центра колеса проводим радиус-вектор в точку контакта \(K\);
• Перпендикулярно построенному радиус-вектору откладываем в масштабе вектор скорости \(V_2\) точки \(K\) колеса;
• Аналогично определяем вектор скорости \(V_1\) точки \(K\) шестерни;
• Разность векторов \(V_1\) и \(V_2\) даст искомый вектор скорости скольжения \(V_s\).

Скорость точки \(K\) определяется как произведение длины радиус-вектора на угловую скорость. Для удобства можно задать угловую скорость шестерни равную 1, тогда угловая скорость колеса по модулю будет равна \(U_{12}=\dfrac{Z_2}{Z_1}\)

Если в процессе работы произойдет уменьшение радиуса окружности вершин, то активный участок линии зацепления станет меньше. В результате уменьшится коэффициент торцевого перекрытия, и, как следствие, приведет к ухудшению плавности работы передачи.

Алгоритм нахождения скорости скольжения был рассмотрен вопросе 29. Из иллюстрации следует, что в полюсе зацепления \(P\) скорость скольжения \(V_s=0\). А максимального значения она достигает в крайних точках \(B_1\) и \(B_2\) активного участка линии зацепления.