Квантовая природа излучения - часть II

Основы квантовой физики: закон Кирхгофа, закон Стефана-Больцмана, формула Рэлея-Джинса и гипотеза М. Планка
Ionium.ru Статьи Квантовая природа излучения - часть II

Основные законы квантовой теории

В данной статье рассмотрим основные законы квантовой теории: закон Кирхгофа, закон Стефана-Больцмана и закон смещения Вина. А также с учетом квантовой гипотезы Планка получим формулы Рэлея-Джинса, Стефана-Больцмана и докажем следствие из формулы Планка - закона смещения Вина.

Ранее были рассмотрены основные понятия квантовой теории - тепловое излючение и его характеристики, а также модель черного тела (см. часть I).

Закон Кирхгофа

Исследование теплового изучения сыграло важную роль в создании квантовой теории света, поэтому необходимо рассмотреть законы, которым оно подчиняется.

Кирхгоф, опираясь на второй закон термодинамики и анализируя условия равновесного излучения в изолированной системе тел, установил количественную связь между спектральной плотностью энергетической светимости и спектральной поглощательной способностью тел.

Закон Кирхгофа

Отношение спектральной плотности энергетической светимости к спектральной поглощательной способности не зависит от природы тела, оно является для всех тел универсальной функцией частоты или длины волны и температуры:

$$\dfrac{R_{\nu,T}}{A_{\nu,T}}=r_{\nu,T}$$

Для черного тела \(A_{\nu,T}^{\text{ч}}\equiv1\), тогда из закона Кирхгофа следует, что \(R_{\nu,T}=r_{\nu,T}\) для черного тела. Таким образом \(r_{\nu,T}\) есть спектральная плотность энергетической светимости черного тела.

Из закона Кирхгофа следует, что для всех тел отношение спектральной плотности энергетической светимости к спектральной поглощательной способности равно спектральной плотности энергетической светимости черного тела при той же температуре и частоте.

Физическая аналогия, наглядно демонстрирующая закон Кирхгофа, заключается в следующем (опыт с походной флягой): пусть имеется фляга, одна сторона которой серебристая, а другая черная. Помещая в флягу воду, нагретую до температуры кипения, с помощью термопары, замеряют скорость изменения температуры спая. При измерениях, проводимых на серебристой поверхности, скорость изменения температуры термопары будет незначительной в отличии от скорости изменения температуры термопары при измерениях на черной стороне. Это объясняется тем, что светлая поверхность почти все тепловое излучение отражает, и, соответственно, излучает меньшее количество теплоты, в отличие от черной поверхности, которая поглощает и излучает большое количество.

Вывод: отношение испускательной способности к поглощательной способности не зависит от типа материала и есть универсальная функция Кирхгофа частоты и температуры.

На основании закона Кирхгофа выражение для энергетической светимости тела можно записать в виде:

$$R_{T}=\int\limits_{0}^{\infty}A_{\nu,T}r_{\nu,T}d\nu$$

Для серого тела:

$$R_{T}^{c}=A_{T}\int\limits_{0}^{\infty}r_{\nu,T}d\nu=A_{T}R_{e}$$

где: \(R_{e}=\int\limits_{0}^{\infty}r_{\nu,T}d\nu\) - энергетическая светимость черного тела (зависит только от температуры).

Закон Кирхгофа описывает только тепловое излучение и является настолько характерным для него, что может быть использован для определения природы излучения. Излучение, которое закону Кирхгофа не подчиняется, не является тепловым.

Законы Стефана-Больцмана и смещения Вина

Нахождение явной зависимости универсальной функции Кирхгофа от частоты и температуры является важной задачей теории теплового излучения. В 1879 году австрийский физик Й.Стефан, а затем в 1884 Л.Больцман применяя законы термодинамики частично решили задачу, установив зависимость энергетической светимости \(R_{e}\) черного тела от температуры.

Закон Стефана-Больцмана

Энергетическая светимость черного тела пропорциональна четвертой степени его термодинамической температуры:

$$R_{e}=\sigma T^{4}$$

где: \(\sigma=5.67\cdot10^{-8}\ \dfrac{\text{Вт}}{\text{м}^{2}\cdot K^{4}}\) - постоянная Стефана-Больцмана.

Закон Стефана-Больцмана определяет зависимость \(R_{e}\) от температуры, однако не дает ответа относительно спектрального состава излучения черного тела. Из экспериментальных кривых зависимость функции \(r_{\lambda,T}\) от длины волны \(\lambda\) при различных температурах (см. рисунок 1) следует, что распределение энергии в спектре черного тела является неравномерным. Все кривые имеют явно выраженный максимум, который по мере повышения температуры смещается в сторону более коротких длин волн.

Зависимость энергетической светимости от длины волны и температуры
Рисунок 1 - Зависимость \(r_{\lambda,T}\) от \(\lambda\)

Площадь, ограниченная кривой зависимости \(r_{\lambda,T}\) от длины волны \(\lambda\) и осью абcцисс, пропорциональна энергетической светимости \(R_{e}\) черного тела и, следовательно, по закону Стефана-Больцмана, четвертой степени температуры.

Немецкий физик В. Вин, используя законы термо- и электродинамики, установил зависимость длины волны \(\lambda_{max}\), соответствующей максимуму функции \(r_{\lambda,T}\) от температуры \(T\).

Закон смещения Вина

Длина волны \(\lambda_{max}\), соответствующая максимальному значению спектральной плотности энергетической светимости \(r_{\lambda,T}\), обратно пропорциональна его термодинамической температуре:

$$\lambda_{max}=\dfrac{b}{T}$$

где: \(b=2.9\cdot10^{-3}\) - постоянная Вина.

Закон Вина объясняет, почему при понижении температуры нагретых тел в их спектре все сильнее преобладает длинноволновое излучение (переход белого каления в красное при остывании металла).

Формула Рэлея-Джинса

Использование методов термо- и электродинамики не дали желаемых результатов. Следующая строгая попытка теоретического вывода зависимости \(r_{\nu,T}\) принадлежит английским ученым Д. Рэлею и Д. Джинсу. На основании методов статистической физики и классических законов о равномерном распределении энергии по степеням свободы для спектральной плотности энергетической светимости черного тела была получена:

Формула Рэлея-Джинса

$$r_{\nu,T}=\dfrac{2\pi\nu^{2}}{c^2}\langle\varepsilon\rangle=\dfrac{2\pi\nu^{2}}{c^2}kT$$

где: \(\langle\varepsilon\rangle=kT\) - средняя энергия осциллятора с собственной частотой \(\nu\).

Для осциллятора, совершающего колебания, средние значения кинетической и потенциальной энергий одинаковы, поэтому средняя энергия каждой степени свободы \(\langle\varepsilon\rangle=kT\).

Расхождение формулы Рэлея-Джинса с экспериментом и законом смещения Вина
Рисунок 2 - Расхождение формулы Рэлея-Джинса с экспериментом и законом смещения Вина

Достаточно быстро при экспериментальной проверке выяснилось, что формула Рэлея-Джинса согласуется с экспериментальными данными только в области достаточно малых частот и больших температур. В области больших частот формула Рэлея-Джинса резко расходится с экспериментом и законом смещения Вина (см. рисунок 2). Теоретические попытки получить закон Стефана-Больцмана из формулы Рэлея-Джинса привели к абсурдному результату. По Рэлею-Джинсу энергетическая светимость черного тела:

$$R_{e}=\int\limits_{0}^{\infty}r_{\nu,T}d\nu=\dfrac{2\pi kT}{c^2}\int\limits_{0}^{\infty}\nu^2d\nu=\infty$$

По закону Стефана-Больцмана \(R_{e}\) пропорциональна четвертой степени температуры, но формула Релея-Джинса не дает сходимости к конечному значению вообще. Это явление получило название ультрафиолетовая катастрофа. В рамках классической физики не удалось объяснить законы распределения энергии в спектре черного тела.

Закон излучения Вина и квантовая гипотеза Планка

В области больших частот хорошо согласуется формула Вина (закон излучения Вина), которую Вин получил из общих теоретических соображений:

$$r_{\nu,T}=C\nu^{3}Ae^{-\dfrac{h\nu}{kT}}$$

где: \(C\), \(A\) - постоянные величины.

В современных обозначениях с использованием постоянной Планка, которая в то время еще не была известна, закон излучения Вина можно записать в виде:

$$r_{\nu_{1},T}=\dfrac{2\pi h\nu^{3}}{c^{2}}e^{-\dfrac{h\nu}{kT}}$$

Следующей важной ступенью развития квантовой физики стала гипотеза, высказанная в 1900 г. немецким физиком М. Планком, которая получила название квантовая гипотеза:

Согласно квантовой гипотезе, атомные осцилляторы излучают энергию не непрерывно, а определенными порциями - квантами, причем энергия кванта пропорциональна частоте колебания:

$$\varepsilon_{0}=h\nu=\dfrac{hc}{\lambda}$$

где: \(h=6.625\cdot10^{-34}\ \text{Дж}\cdot c\) - постоянная Планка.

Атомный осциллятор испускает излучение порциями, поэтому энергия осциллятора \(\varepsilon\) может принимать лишь определенные дискретные значения, кратные целому числу элементарных порций энергии \(\varepsilon_{0}\):

$$\varepsilon=nh\nu\ \ \ \ (n=0,1,2,...)$$

Планк допустил, что распределение осцилляторов по возможным дискретным состояниям подчиняется распределению Больцмана, поэтому средняя энергия осциллятора:

$$\langle\varepsilon\rangle=\dfrac{h\nu}{e^{\frac{h\nu}{kT}}-1}$$

Спектральная плотность энергетической светимости черного тела:

$$r_{\nu,T}=\dfrac{2\pi h\nu^{3}}{c^{2}}\dfrac{1}{e^{\frac{h\nu}{kT}}-1}(*)$$

Заслуга Планка в том, что ему удалось вывести выражение для универсальной функции Кирхгофа, которая, как оказалось, блестяще согласуется с экспериментальными данными по распределению энергии в спектрах излучения черного тела во всем интервале частот и температур.

Вывод формулы Рэлея-Джинса из формулы Планка в области малых частот

В области малых частот (при \(h\nu \ll kT\), энергия кванта очень мала по сравнению с энергией теплового движения \(kT\)), формула Планка совпадает с формулой Рэлея-Джинса.

Разложим экспоненциальную функцию в ряд, ограничившись для рассмотрения двумя членами:

$$e^{\frac{h\nu}{kT}}\approx1+\dfrac{h\nu}{kT}$, $e^{\frac{h\nu}{kT}}-1\approx\dfrac{h\nu}{kT}$$

Подставим в формула Планка (*), получим:

$$r_{\nu,T}=\dfrac{2\pi h\nu^{3}}{c^{2}}\dfrac{1}{\frac{h\nu}{kT}}=\dfrac{2\pi\nu^{2}}{c^2}kT$$

Получена формула Рэлея-Джинса.

Вывод формулы Стефана-Больцмана из формулы Планка

Согласно (*):

$$R_{e}=\int\limits_{0}^{\infty}r_{\nu,T}d\nu=\int\limits_{0}^{\infty}\dfrac{2\pi h\nu^{3}}{c^{2}}\dfrac{1}{e^{\frac{h\nu}{kT}}-1}$$

Введем переменную:

$$x=\dfrac{h\nu}{kT};\quad dx=\dfrac{hd\nu}{kT};\quad d\nu=\dfrac{kTdx}{h}$$

Подставим значение в формулу для \(R_{e}\):

$$R_{e}=\dfrac{2\pi k^{4}}{c^{2}h^{3}}T^{4}\int\limits_{0}^{\infty}\dfrac{x^{3}}{e^{x}-1}dx=\sigma T^{4}$$

где:

$$\sigma=\dfrac{2\pi k^{4}}{c^{2}h^{3}}\int\limits_{0}^{\infty}\dfrac{x^{3}}{e^{x}-1}dx=\dfrac{2\pi^{5}k^{4}}{15c^{2}h^{3}},$$

так как

$$\int\limits_{0}^{\infty}\dfrac{x^{3}}{e^{x}-1}dx=\dfrac{\pi^{4}}{15}$$

Далее возможно численно рассчитать значение постоянной Стефана-Больцмана, которая хорошо согласуется с экспериментальными данными.

Вывод закона смещения Вина из формулы Планка

С помощью спектральной плотности энергетической светимости в виде функции длины волны и (*), получаем:

$$r_{\lambda,T}=\dfrac{c}{\lambda^{2}}r_{\nu,T}=\dfrac{2\pi c^{2}h }{\lambda^{5}}\dfrac{1}{e^{\frac{h\nu}{kT}}-1}$$

Возьмем частную производную:

$$\dfrac{\partial r_{\lambda,T}}{\partial\lambda}=\dfrac{2\pi c^{2}h}{\lambda^{6}(e^{\frac{hc}{kT\lambda}}-1)} (\dfrac{\dfrac{hc}{kT\lambda}e^{\frac{hc}{kT\lambda}}}{e^\frac{hc}{kT\lambda}-1}-5)$$

Найдем значение \(\lambda_{max}\), при котором функция достигает максимума, приравняв нулю эту производную. Введем:

$$x=\dfrac{hc}{kT\lambda_{max}},$$

получим уравнение:

$$xe^{x}-5(e^{x}-1)=0$$

Это трансцендентное уравнение, найдем его решение численным методом (см. рисунок 3)

К решению уравнения
Рисунок 3 - К решению уравнения

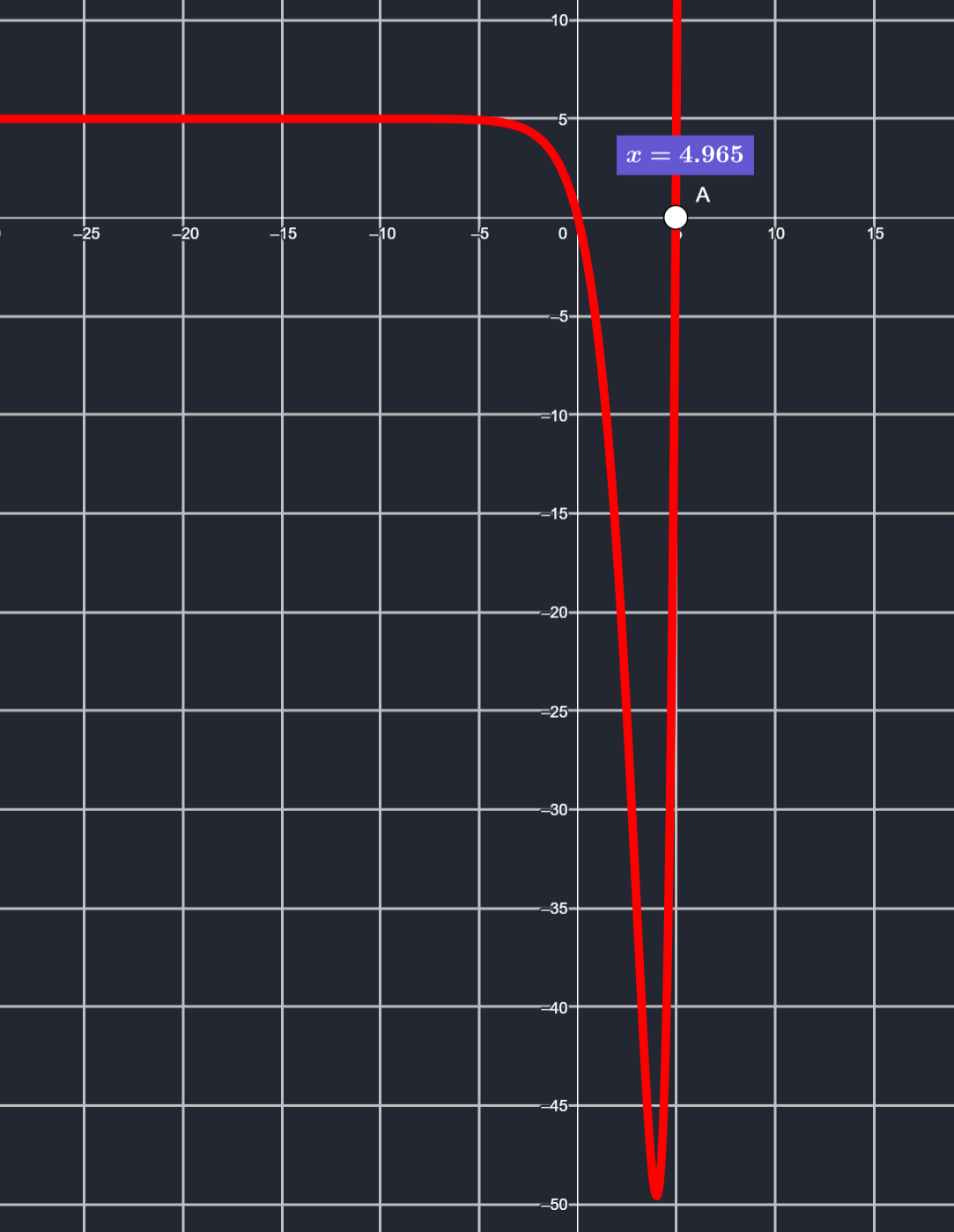
следовательно:

$$\dfrac{hc}{kT\lambda_{max}}=4.965,$$

откуда:

$$T\lambda_{max}=\dfrac{hc}{4.965}=b$$

Получен закон смещения Вина.